Set reproduction parameters

Sets the proportion of the total energy available for reproduction and growth that is invested into reproduction as a function of the size of the individual and sets additional density dependence.

Usage

setReproduction(
  params,
  maturity = NULL,
  repro_prop = NULL,
  reset = FALSE,
  RDD = NULL,
  ...
)

getMaturityProportion(params)

maturity(params)

maturity(params) <- value

getReproductionProportion(params)

repro_prop(params)

repro_prop(params) <- value

Arguments

params: A MizerParams object
maturity: Optional. An array (species x size) that holds the proportion of individuals of each species at size that are mature. If not supplied, a default is set as described in the section "Setting reproduction".
repro_prop: Optional. An array (species x size) that holds the proportion of consumed energy that a mature individual allocates to reproduction for each species at size. If not supplied, a default is set as described in the section "Setting reproduction".
reset: If set to TRUE, then both maturity and repro_prop will be reset to the value calculated from the species parameters, even if they were previously overwritten with custom values. If set to FALSE (default) then a recalculation from the species parameters will take place only if no custom values have been set.
RDD: The name of the function calculating the density-dependent reproduction rate from the density-independent rate. Defaults to "BevertonHoltRDD()".
...: Unused
value: .

Value

setReproduction(): A MizerParams object with updated reproduction parameters.

getMaturityProportion() or equivalently `maturity(): An array (species x size) that holds the proportion of individuals of each species at size that are mature.

getReproductionProportion() or equivalently repro_prop(): An array (species x size) that holds the proportion of consumed energy that a mature individual allocates to reproduction for each species at size. For sizes where the maturity proportion is zero, also the reproduction proportion is returned as zero.

Setting reproduction

For each species and at each size, the proportion $\psi$ of the available energy that is invested into reproduction is the product of two factors: the proportion maturity of individuals that are mature and the proportion repro_prop of the energy available to a mature individual that is invested into reproduction. There is a size w_repro_max at which all the energy is invested into reproduction and therefore all growth stops. There can be no fish larger than w_repro_max. If you have not specified the w_repro_max column in the species parameter data frame, then the maximum size w_max is used instead.

Maturity ogive

If the the proportion of individuals that are mature is not supplied via the maturity argument, then it is set to a sigmoidal maturity ogive that changes from 0 to 1 at around the maturity size: $${\tt maturity}(w) = \left[1+\left(\frac{w}{w_{mat}}\right)^{-U}\right]^{-1}.$$ (To avoid clutter, we are not showing the species index in the equations, although each species has its own maturity ogive.) The maturity weights are taken from the w_mat column of the species_params data frame. Any missing maturity weights are set to 1/4 of the maximum weight in the w_max column.

The exponent $U$ determines the steepness of the maturity ogive. By default it is chosen as $U = 10$, however this can be overridden by including a column w_mat25 in the species parameter dataframe that specifies the weight at which 25% of individuals are mature, which sets $U = \log(3) / \log(w_{mat} / w_{mat25}).$

The sigmoidal function given above would strictly reach 1 only asymptotically. Mizer instead sets the function equal to 1 already at a size taken from the w_repro_max column in the species parameter data frame, if it exists, or otherwise from the w_max column. Also, for computational simplicity, any proportion smaller than 1e-8 is set to 0.

Investment into reproduction

If the the energy available to a mature individual that is invested into reproduction is not supplied via the repro_prop argument, it is set to the allometric form $${\tt repro\_prop}(w) = \left(\frac{w}{w_{\tt{repro\_max}}}\right)^{m-n}.$$ Here $n$ is the scaling exponent of the energy income rate. Hence the exponent $m$ determines the scaling of the investment into reproduction for mature individuals. By default it is chosen to be $m = 1$ so that the rate at which energy is invested into reproduction scales linearly with the size. This default can be overridden by including a column m in the species parameter dataframe. The maximum sizes are taken from the w_repro_max column in the species parameter data frame, if it exists, or otherwise from the w_max column.

The total proportion of energy invested into reproduction of an individual of size $w$ is then $$\psi(w) = {\tt maturity}(w){\tt repro\_prop}(w)$$

Reproductive efficiency

The reproductive efficiency $\epsilon$, i.e., the proportion of energy allocated to reproduction that results in egg biomass, is set through the erepro column in the species_params data frame. If that is not provided, the default is set to 1 (which you will want to override). The offspring biomass divided by the egg biomass gives the rate of egg production, returned by getRDI(): $$R_{di} = \frac{\epsilon}{2 w_{min}} \int N(w) E_r(w) \psi(w) \, dw$$

Density dependence

The stock-recruitment relationship is an emergent phenomenon in mizer, with several sources of density dependence. Firstly, the amount of energy invested into reproduction depends on the energy income of the spawners, which is density-dependent due to competition for prey. Secondly, the proportion of larvae that grow up to recruitment size depends on the larval mortality, which depends on the density of predators, and on larval growth rate, which depends on density of prey.

Finally, to encode all the density dependence in the stock-recruitment relationship that is not already included in the other two sources of density dependence, mizer puts the the density-independent rate of egg production through a density-dependence function. The result is returned by getRDD(). The name of the density-dependence function is specified by the RDD argument. The default is the Beverton-Holt function BevertonHoltRDD(), which requires an R_max column in the species_params data frame giving the maximum egg production rate. If this column does not exist, it is initialised to Inf, leading to no density-dependence. Other functions provided by mizer are RickerRDD() and SheperdRDD() and you can easily use these as models for writing your own functions.

Examples

# \donttest{
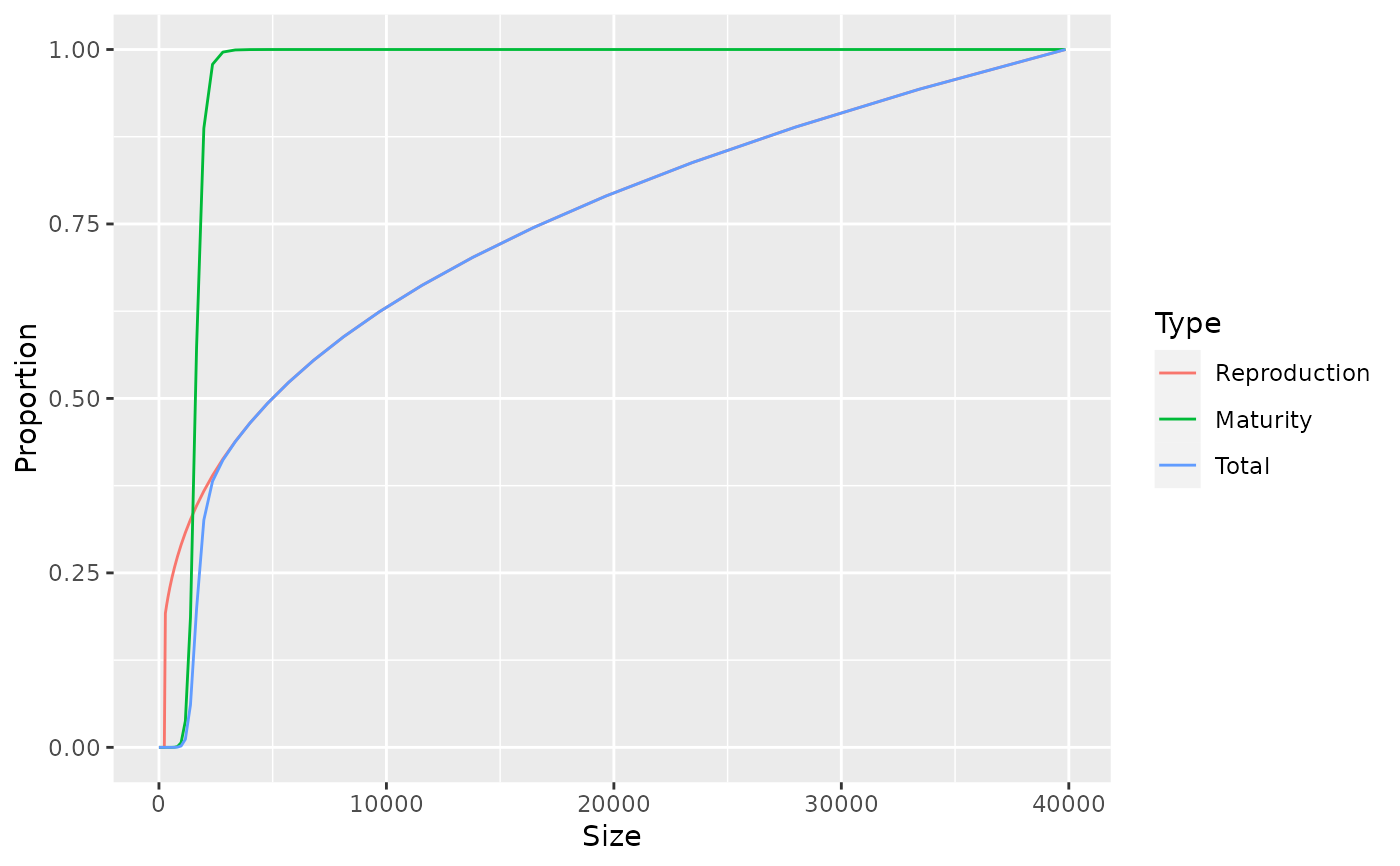
# Plot maturity and reproduction ogives for Cod in North Sea model
maturity <- getMaturityProportion(NS_params)["Cod", ]
repro_prop <- getReproductionProportion(NS_params)["Cod", ]
df <- data.frame(Size = w(NS_params), 
                 Reproduction = repro_prop, 
                 Maturity = maturity, 
                 Total = maturity * repro_prop)
dff <- melt(df, id.vars = "Size", 
            variable.name = "Type", 
            value.name = "Proportion")
library(ggplot2)
ggplot(dff) + geom_line(aes(x = Size, y = Proportion, colour = Type))

# }