
A Multi-Species Model of the North Sea
Source:vignettes/a_multispecies_model_of_the_north_sea.Rmd
a_multispecies_model_of_the_north_sea.RmdIn this section we try to pull everything together with an extended example of a multispecies model for the North Sea. First we will set up the model, project it through time using historical levels of fishing effort, and then examine the results. We then run two different future projection scenarios.
Setting up the North Sea model
The first job is to set up the MizerParams object for
the North Sea model. In the previous multispecies examples we have
already been using the life-history parameters and the interaction
matrix for the North Sea model. We will use them again here but will
make some changes. In particular we set up the fishing gears
differently.
The species in the model are: Sprat, Sandeel, N.pout, Herring, Dab,
Whiting, Sole, Gurnard, Plaice, Haddock, Cod, Saithe, which account for
about 90% of the total biomass of all species sampled by research trawl
surveys in the North Sea. The NS_species_params object that
comes as an example with the mizer package is a data.frame with columns
for species, w_max, w_mat,
beta, sigma, k_vb and
R_max.
NS_species_params## species w_max w_mat beta sigma k_vb R_max w_inf
## 1 Sprat 33.0 13 51076 0.8 0.681 7.38e+11 33.0
## 2 Sandeel 36.0 4 398849 1.9 1.000 4.10e+11 36.0
## 3 N.pout 100.0 23 22 1.5 0.849 1.05e+13 100.0
## 4 Herring 334.0 99 280540 3.2 0.606 1.11e+12 334.0
## 5 Dab 324.0 21 191 1.9 0.536 1.12e+10 324.0
## 6 Whiting 1192.0 75 22 1.5 0.323 5.48e+11 1192.0
## 7 Sole 866.0 78 381 1.9 0.284 3.87e+10 866.0
## 8 Gurnard 668.0 39 283 1.8 0.266 1.65e+12 668.0
## 9 Plaice 2976.0 105 113 1.6 0.122 4.08e+14 2976.0
## 10 Haddock 4316.5 165 558 2.1 0.271 1.84e+12 4316.5
## 11 Cod 39851.3 1606 66 1.3 0.216 8.26e+09 39851.3
## 12 Saithe 39658.6 1076 40 1.1 0.175 1.12e+11 39658.6We have seen before that only having these columns in the species
data.frame is sufficient to make a MizerParams object. Any
missing columns will be filled with default values by the
MizerParams constructor. For example, the data.frame does
not include columns for h or gamma. This means
that they will be estimated using the k_vb column.
We will use the default density dependence in the reproduction rate,
which is the Beverton-Holt shape. This requires a column
R_max in the species data.frame which contains the maximum
reproduction rate for each species. This column is already in the
NS_species_params data.frame. The values were found through
a calibration process which is not covered here but will be described in
a separate tutorial.
At the moment we are not providing any information on the selectivity
of the gears for the species. By default, the selectivity function is a
knife-edge which only takes a single argument,
knife_edge_size. In this model we want the selectivity
pattern to be a sigmoid shape which more accurately reflects the
selectivity pattern of trawlers in the North Sea. The sigmoid
selectivity function is expressed in terms of length rather than weight
and uses the parameters l25 and l50, which are
the lengths at which 25% and 50% of the stock is selected. The length
based sigmoid selectivity looks like:
\[\begin{equation} % {#eq:trawl_sel} S_l = \frac{1}{1 + \exp(S1 - S2\ l)} \end{equation}\]
where \(l\) is the length of an individual, \(S_l\) is the selectivity at length, \(S2 = \log(3) / (l50 - l25)\) and \(S1 = l50 \cdot S2\).
This selectivity function is included in mizer as
sigmoid_length(). You can see the help page for more
details. As the mizer model is weight based, and this selectivity
function is length based, it uses the length-weight parameters
a and b to convert between length and weight
using the standard relation \(w = a
l^b\). These species parameters need to be added as columns to
the NS_species_params data frame.
NS_species_params$a <- c(0.007, 0.001, 0.009, 0.002, 0.010, 0.006, 0.008, 0.004,
0.007, 0.005, 0.005, 0.007)
NS_species_params$b <- c(3.014, 3.320, 2.941, 3.429, 2.986, 3.080, 3.019, 3.198,
3.101, 3.160, 3.173, 3.075)sigmoid_length() has the arguments l25 and
l50. As explained in the section on fishing
gears and selectivity, the arguments of the selectivity function
need to be in the gear parameter data frame. We also need a column
specifying the name of the selectivity function we wish to use. Note it
would probably be easier to put this data into a *.csv file and then
read it in rather than type it in by hand like we do here:
gear_params <-
data.frame(species = NS_species_params$species,
gear = NS_species_params$species,
sel_func = "sigmoid_length",
l25 = c(7.6, 9.8, 8.7, 10.1, 11.5, 19.8, 16.4, 19.8, 11.5,
19.1, 13.2, 35.3),
l50 = c(8.1, 11.8, 12.2, 20.8, 17.0, 29.0, 25.8, 29.0, 17.0,
24.3, 22.9, 43.6))
gear_params## species gear sel_func l25 l50
## 1 Sprat Sprat sigmoid_length 7.6 8.1
## 2 Sandeel Sandeel sigmoid_length 9.8 11.8
## 3 N.pout N.pout sigmoid_length 8.7 12.2
## 4 Herring Herring sigmoid_length 10.1 20.8
## 5 Dab Dab sigmoid_length 11.5 17.0
## 6 Whiting Whiting sigmoid_length 19.8 29.0
## 7 Sole Sole sigmoid_length 16.4 25.8
## 8 Gurnard Gurnard sigmoid_length 19.8 29.0
## 9 Plaice Plaice sigmoid_length 11.5 17.0
## 10 Haddock Haddock sigmoid_length 19.1 24.3
## 11 Cod Cod sigmoid_length 13.2 22.9
## 12 Saithe Saithe sigmoid_length 35.3 43.6Note that we have set up a gear column so that each
species will be caught by a separate gear named after the species.
In this model we are interested in projecting forward using
historical fishing mortalities. The historical fishing mortality from
1967 to 2010 for each species is stored in the csv file
NS_f_history.csv included in the package. As before, we can
use read.csv() to read in the data. This reads the data in
as a data.frame. We want this to be a matrix
so we use the as() function:
f_location <- system.file("extdata", "NS_f_history.csv", package = "mizer")
f_history <- as(read.csv(f_location, row.names = 1), "matrix")We can take a look at the first years of the data:
head(f_history)## Sprat Sandeel N.pout Herring Dab Whiting Sole Gurnard
## 1967 0 0 0 1.0360279 0.09417655 0.8294528 0.6502019 0
## 1968 0 0 0 1.7344576 0.07376065 0.8008995 0.7831250 0
## 1969 0 0 0 1.4345001 0.07573638 1.3168280 0.8744095 0
## 1970 0 0 0 1.4342405 0.10537236 1.3473505 0.6389915 0
## 1971 0 0 0 1.8234973 0.08385884 0.9741884 0.8167561 0
## 1972 0 0 0 0.9033768 0.09044461 1.3148588 0.7382834 0
## Plaice Haddock Cod Saithe
## 1967 0.4708827 0.7428694 0.6677456 0.4725102
## 1968 0.3688033 0.7084553 0.6994389 0.4270201
## 1969 0.3786819 1.3302821 0.6917888 0.3844648
## 1970 0.5268618 1.3670695 0.7070891 0.5987086
## 1971 0.4192942 0.9173131 0.7737543 0.4827822
## 1972 0.4522231 1.3279087 0.8393267 0.5796321Fishing mortality is calculated as the product of selectivity,
catchability and fishing effort. The values in f_history
are absolute levels of fishing mortality. We have seen that the fishing
mortality in the mizer simulations is driven by the fishing
effort argument passed to the project() function. Therefore
if we want to project forward with historical fishing levels, we need to
provide project() with effort values that will result in
these historical fishing mortality levels.
One of the model parameters that we have not really considered so far
is catchability. Catchability is a scalar parameter used to
modify the fishing mortality at size given the selectivity at size and
effort of the fishing gear. By default catchability has a value of 1,
meaning that an effort of 1 results in a fishing mortality of 1 for a
fully selected species. When considering the historical fishing
mortality, one option is therefore to leave catchability at 1 for each
species and then use the f_history matrix as the fishing
effort. However, an alternative method is to use the effort relative to
a chosen reference year. This can make the effort levels used in the
model more meaningful. Here we use the year 1990 as the reference year.
If we set the catchability of each species to be the same as the fishing
mortality in 1990 then an effort of 1 in 1990 will result in the fishing
mortality being what it was in 1990. The effort in the other years will
be relative to the effort in 1990.
gear_params$catchability <- as.numeric(f_history["1990", ])Considering the other model parameters, we will use default values
for all of the other parameters apart from kappa, the
carrying capacity of the resource spectrum (see see the section on
resource density). This was estimated along with the values
R_max as part of the calibration process.
We now have all the information we need to create the
MizerParams object using the species parameters
data.frame.
params <- newMultispeciesParams(NS_species_params,
interaction = inter,
kappa = 9.27e10,
gear_params = gear_params)## Because you have n != p, the default value for `h` is not very good.
## Because the age at maturity is not known, I need to fall back to using
## von Bertalanffy parameters, where available, and this is not reliable.
## No ks column so calculating from critical feeding level.
## Using z0 = z0pre * w_max ^ z0exp for missing z0 values.
## Using f0, h, lambda, kappa and the predation kernel to calculate gamma.Setting up and running the simulation
As we set our catchability to be the level of fishing mortality in
1990, before we can run the projection we need to rescale the effort
matrix to get a matrix of efforts relative to 1990. To do this we want
to rescale the f_history object to 1990 so that the
relative fishing effort in 1990 = 1. This is done using R function
sweep(). We then check a few rows of the effort matrix to
check this has happened:
relative_effort <- sweep(f_history, 2, f_history["1990", ], "/")
relative_effort[as.character(1988:1992), ]## Sprat Sandeel N.pout Herring Dab Whiting Sole
## 1988 0.8953804 1.2633229 0.8953804 1.214900 1.176678 0.9972560 1.2786517
## 1989 1.1046196 1.2931034 1.1046196 1.232790 1.074205 0.8797926 0.9910112
## 1990 1.0000000 1.0000000 1.0000000 1.000000 1.000000 1.0000000 1.0000000
## 1991 1.1902174 0.8814002 1.1902174 1.108016 1.143110 0.8096927 1.0044944
## 1992 1.2500000 0.8500522 1.2500000 1.316576 1.113074 0.7718676 0.9505618
## Gurnard Plaice Haddock Cod Saithe
## 1988 0.0000000 1.176678 0.9946140 1.045964 1.0330579
## 1989 0.0000000 1.074205 0.8545781 1.060538 1.1223140
## 1990 1.0000000 1.000000 1.0000000 1.000000 1.0000000
## 1991 0.8096927 1.143110 0.7971275 1.001121 0.9619835
## 1992 0.7718676 1.113074 0.8797127 0.970852 1.0528926We could just project forward with these relative efforts. However, the population dynamics in the early years will be strongly determined by the initial population abundances (known as the transient behaviour - essentially the initial behaviour before the long term dynamics are reached). As this is ecology, we don’t know what the initial abundance are. One way around this is to project forward at a constant fishing mortality equal to the mortality in the first historical year until equilibrium is reached. We then use this steady state as the initial state for the simulation. This approach reduces the impact of transient dynamics.
params <- projectToSteady(params, effort = relative_effort["1967", ])## Convergence was achieved in 24 years.We now have our parameter object and out matrix of efforts relative
to 1990. We use this effort matrix as the effort argument
to the project() function. We use dt = 0.25
(the simulation will run faster than with the default value of 0.1, but
tests show that the results are still stable) and save the results every
year.
sim <- project(params, effort = relative_effort, dt = 0.25, t_save = 1)Plotting the results, we can see how the biomasses of the stocks change over time.
plotBiomass(sim)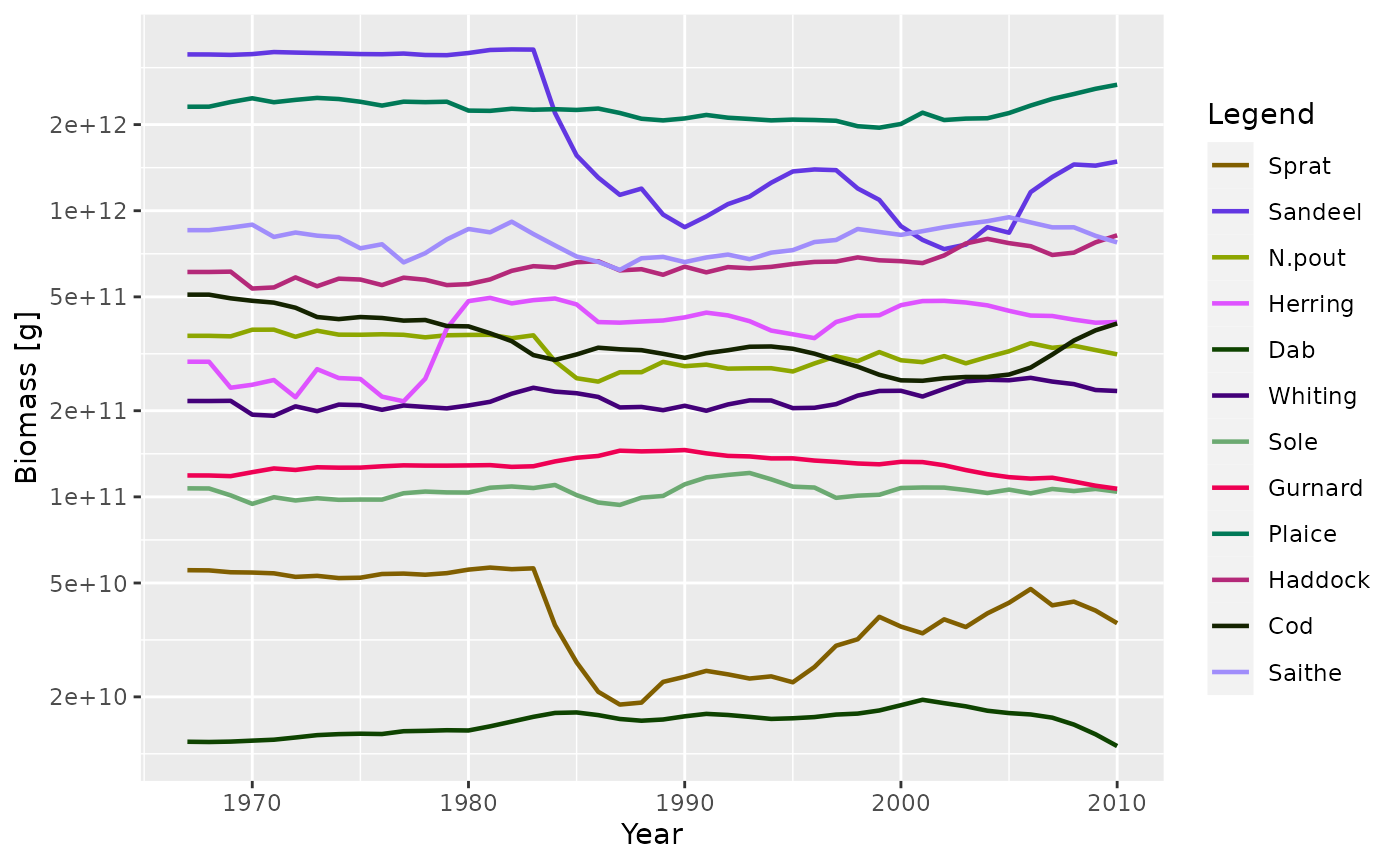
To explore the state of the community it is useful to calculate indicators of the unexploited community. Therefore we also project forward to the steady state with 0 fishing effort.
sim0 <- projectToSteady(params, effort = 0, return_sim = TRUE)## Convergence was achieved in 42 years.Exploring the model outputs
Here we look at some of the ways the results of the simulation can be
explored. We calculate the community indicators
mean maximum weight, mean individual weight,
community slope and the large fish indicator
(LFI) over the simulation period, and compare them to the unexploited
values. We also compare the simulated values of the LFI to a community
target based on achieving a high proportion of the unexploited value of
the LFI of \(0.8 LFI_{F=0}\).
The indicators are calculated using the functions described in the section about indicator functions. Here we calculate the LFI and the other community indicators for the unexploited community. When calculating these indicators we only include demersal species and individuals in the size range 10 g to 100 kg, and the LFI is based on species larger than 40 cm. Each of these functions returns a time series. We are interested only in the equilibrium unexploited values so we just select the final time step.
demersal_species <- c("Dab", "Whiting", "Sole", "Gurnard", "Plaice",
"Haddock", "Cod", "Saithe")
final <- idxFinalT(sim0)
lfi0 <- getProportionOfLargeFish(sim0, species = demersal_species,
min_w = 10, max_w = 100e3,
threshold_l = 40)[[final]]
mw0 <- getMeanWeight(sim0, species = demersal_species,
min_w = 10, max_w = 100e3)[[final]]
mmw0 <- getMeanMaxWeight(sim0, species = demersal_species,
min_w = 10, max_w = 100e3)[final, "mmw_biomass"]
slope0 <- getCommunitySlope(sim0, species = demersal_species,
min_w = 10, max_w = 100e3)[final, "slope"]We also calculate the time series of these indicators for the exploited community:
lfi <- getProportionOfLargeFish(sim, species = demersal_species,
min_w = 10, max_w = 100e3,
threshold_l = 40)
mw <- getMeanWeight(sim, species = demersal_species,
min_w = 10, max_w = 100e3)
mmw <- getMeanMaxWeight(sim, species = demersal_species, min_w = 10,
max_w = 100e3)[, "mmw_biomass"]
slope <- getCommunitySlope(sim, species = demersal_species, min_w = 10,
max_w = 100e3)[, "slope"]We can plot the exploited and unexploited indicators, along LFI
reference level. Here we do it using ggplot2 which uses
data.frames. We make three data.frames (one for the time series, one for
the unexploited levels and one for the reference level): Each data.frame
is a data.frame of each of the measures, stacked on top of each
other.
library(ggplot2)
years <- 1967:2010
# Simulated data
community_plot_data <- rbind(
data.frame(year = years, measure = "LFI", data = lfi),
data.frame(year = years, measure = "Mean Weight", data = mw),
data.frame(year = years, measure = "Mean Max Weight", data = mmw),
data.frame(year = years, measure = "Slope", data = slope))
# Unexploited data
community_unfished_data <- rbind(
data.frame(year = years, measure = "LFI", data = lfi0),
data.frame(year = years, measure = "Mean Weight", data = mw0),
data.frame(year = years, measure = "Mean Max Weight", data = mmw0),
data.frame(year = years, measure = "Slope", data = slope0))
# Reference level
community_reference_level <-
data.frame(year = years, measure = "LFI", data = lfi0 * 0.8)
# Build up the plot
ggplot(community_plot_data) +
geom_line(aes(x = year, y = data)) +
facet_wrap(~measure, scales = "free") +
geom_line(aes(x = year, y = data), linetype = "dashed",
data = community_unfished_data) +
geom_line(aes(x = year, y = data), linetype = "dotted",
data = community_reference_level)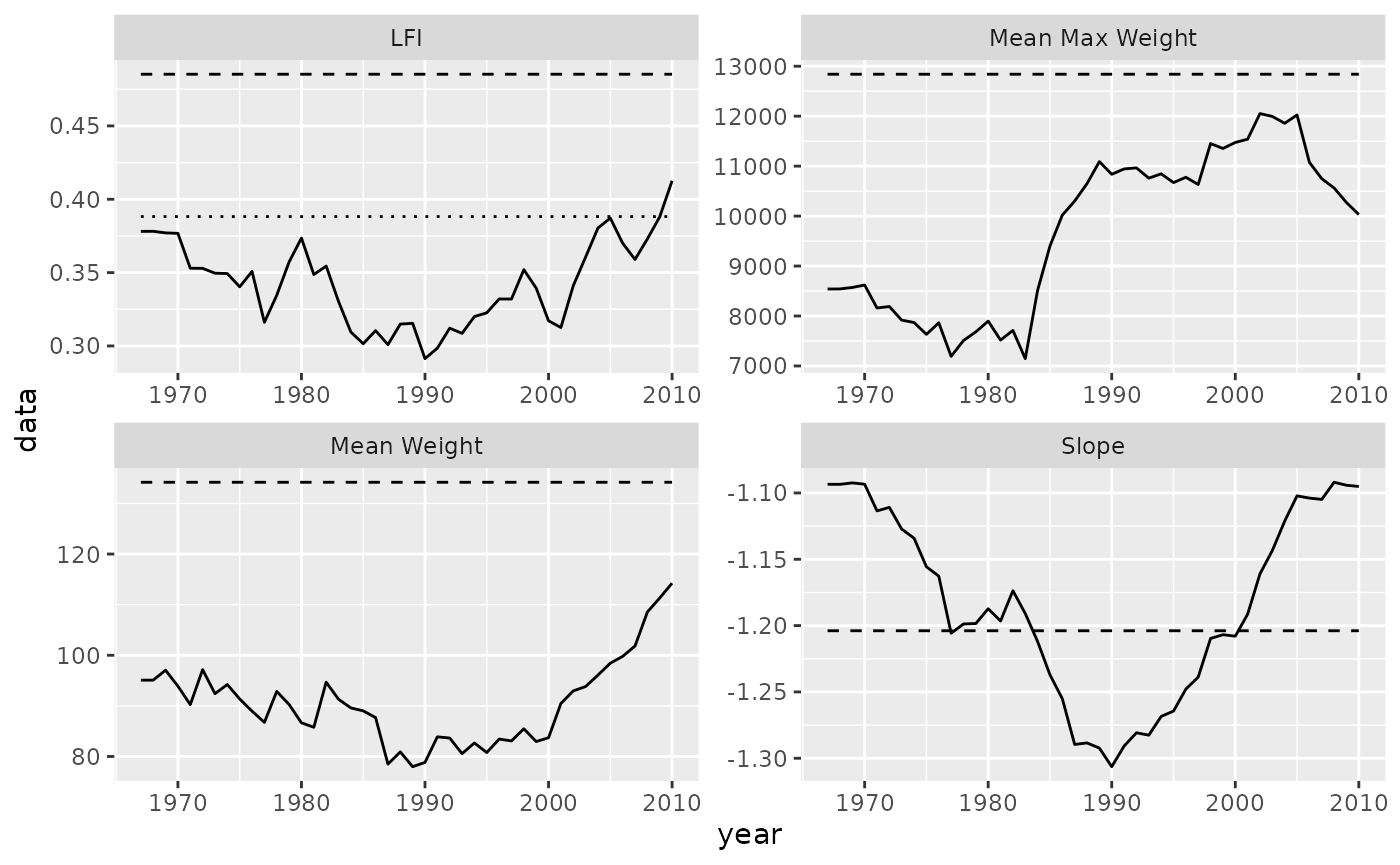
Historical (solid) and unexploited (dashed) and reference (dotted) community indicators for the North Sea multispecies model.
According to our simulations, historically the LFI in the North Sea has been below the reference level.
Future projections
As well as investigating the historical simulations, we can run projections into the future. Here we run two projections to 2050 with different fishing scenarios.
- Continue fishing at 2010 levels (the status quo scenario).
- From 2010 to 2015 linearly change the fishing mortality to approach \(F_{MSY}\) and then continue at \(F_{MSY}\) until 2050.
Rather than looking at community indicators here, we will calculate the SSB of each species in the model and compare the projected levels to a biodiversity target based on the reference point \(0.1 SSB_{F=0}.\)
Before we can run the simulations, we need to set up arrays of future
effort. We will continue to use effort relative to the level in 1990.
Here we build on our existing array of relative effort to make an array
for the first scenario. Note the use of the t() command to
transpose the array. This is needed because R recycles by rows, so we
need to build the array with the dimensions rotated to start with. We
make an array of the future effort, and then bind it underneath the
relative_effort array used in the previous section.
scenario1 <- t(array(relative_effort["2010", ], dim = c(12, 40),
dimnames = list(NULL, year = 2011:2050)))
scenario1 <- rbind(relative_effort, scenario1)The relative effort array for the second scenario is more complicated to make and requires a little bit of R gymnastics (it might be easier for you to prepare this in a spreadsheet and read it in). For this one we need values of \(F_{MSY}\).
fmsy <- c(Sprat = 0.2, Sandeel = 0.2, N.pout = 0.2, Herring = 0.25, Dab = 0.2,
Whiting = 0.2, Sole = 0.22, Gurnard = 0.2, Plaice = 0.25, Haddock = 0.3,
Cod = 0.19, Saithe = 0.3)
scenario2 <- t(array(fmsy, dim = c(12, 40),
dimnames = list(NULL, year = 2011:2050)))
scenario2 <- rbind(relative_effort, scenario2)
for (sp in dimnames(scenario2)[[2]]) {
scenario2[as.character(2011:2015), sp] <- scenario2["2010", sp] +
(((scenario2["2015", sp] - scenario2["2010", sp]) / 5) * 1:5)
}We are now ready to project the two scenarios.
sim1 <- project(params, effort = scenario1, dt = 0.25)
sim2 <- project(params, effort = scenario2, dt = 0.25)We can now compare the projected SSB values in both scenarios to the
biodiversity reference points. First we calculate the biodiversity
reference points (from the final time step in the unexploited
sim0 simulation):
ssb0 <- getSSB(sim0)[final, ]Now we build a data.frame of the projected SSB for each species. We
make use of the melt() function to transform arrays into
data frames.
years <- 1967:2050
ssb1_df <- melt(getSSB(sim1))
ssb2_df <- melt(getSSB(sim2))
ssb_df <- rbind(
cbind(ssb1_df, scenario = "Status quo"),
cbind(ssb2_df, scenario = "Fmsy"))
ssb_unexploited_df <- cbind(expand.grid(
sp = names(ssb0),
time = 1967:2050),
value = as.numeric(ssb0),
scenario = "Unexploited")
ssb_reference_df <- cbind(expand.grid(
sp = names(ssb0),
time = 1967:2050),
value = as.numeric(ssb0 * 0.1),
scenario = "Reference")
ssb_all_df <- rbind(ssb_df, ssb_unexploited_df, ssb_reference_df)
colours <- c("Status quo" = "red", "Fmsy" = "yellow",
"Unexploited" = "blue", "Reference" = "purple")
ggplot(ssb_all_df) +
geom_line(aes(x = time, y = value, colour = scenario)) +
facet_wrap(~sp, scales = "free", nrow = 4) +
theme(legend.position = "none") +
scale_colour_manual(values = colours)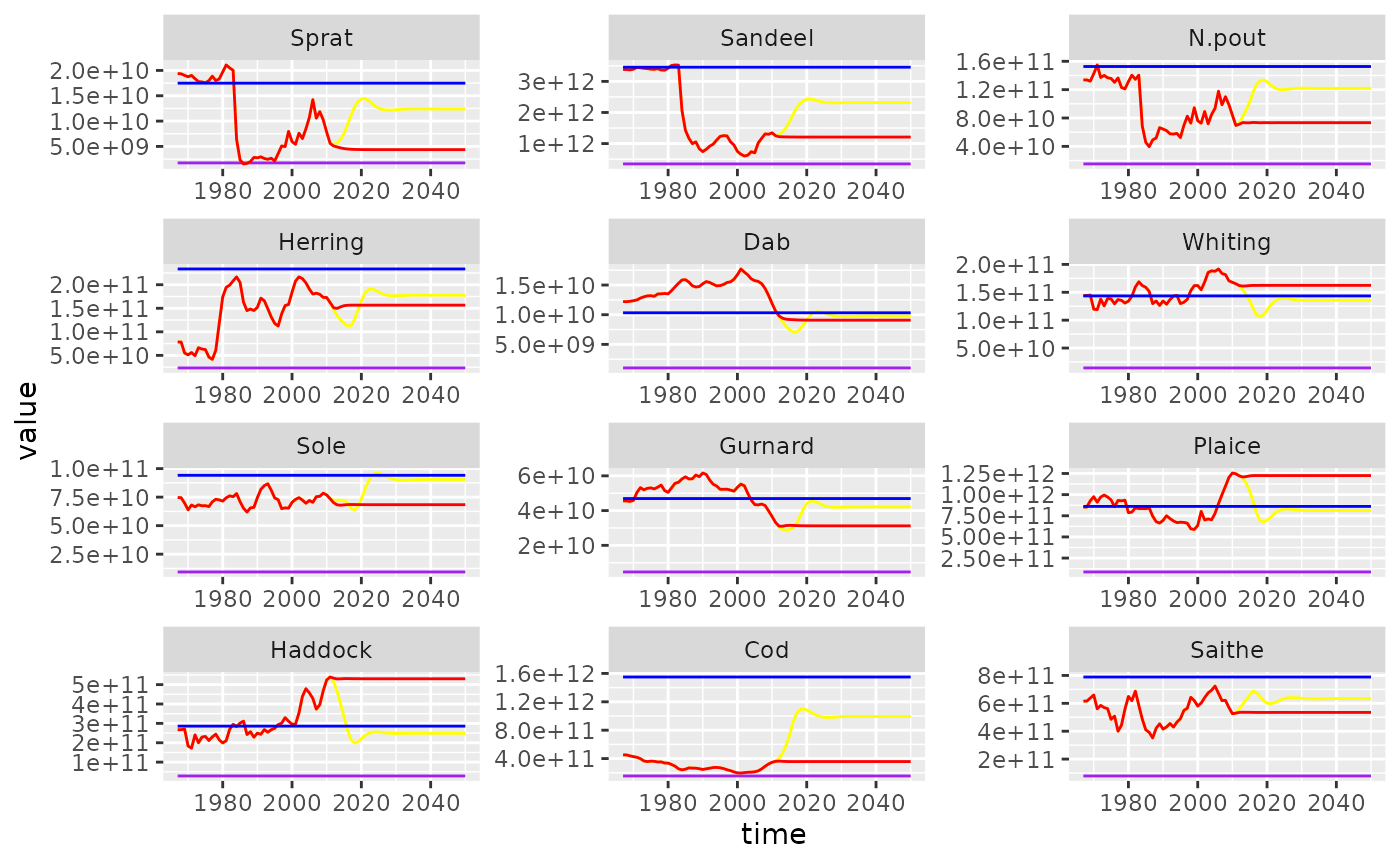
Historical and projected SSB under two fishing scenarios. Status quo (red), Fmsy (yellow). Unexploited (blue) and reference levels (purple) are also shown.